数制和码制
数制(Number System)是表示数字的规则体系,它主要由基数(Radix)和数码(Digit)两个基本要素构成。在多位数中,每个位置的数码都对应一个权(Weight),数值的大小由各位数码与其权值的乘积之和决定。
1. 常见数制
为了清晰地比较,我们将各个数制的核心要素和特点进行结构化展示。
1. 十进制 (Decimal, D)
- 基数: 10
- 数码: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- 特点: 日常生活中最常用的计数系统,规则为“逢十进一”。
2. 二进制 (Binary, B)
- 基数: 2
- 数码: 0, 1
- 特点: 数字电路和计算机系统的基础。其运算规则为“逢二进一”。缺点是表示数值时位数通常很长,不便于人类读写。
3. 八进制 (Octal, O)
- 基数: 8 (即 2³)
- 数码: 0, 1, 2, 3, 4, 5, 6, 7
- 特点: 作为二进制数的一种紧凑表示形式。每一位八进制数可以精确地等效于三位二进制数(例如:(7)₈ = (111)₂),从而简化了二进制数据的书写和阅读
4. 十六进制 (Hexadecimal, H)
- 基数: 16 (即 2⁴)
- 数码: 0-9 以及 A, B, C, D, E, F (分别代表10到15)
- 特点: 计算机领域最常用的二进制紧凑表示法。每一位十六进制数可以精确地等效于四位二进制数(例如:(F)₁₆ = (1111)₂),是目前表示二进制数据最主流、最高效的方式
2. 不同数制的转换
1. n进制 → 十进制
将任意进制数的每一位数值乘以其对应的权(基数的相应次幂),然后将所有乘积相加,即可得到其等值的十进制数。
-
二进制转十进制
(11011.101)₂ = 1×2⁴ + 1×2³ + 0×2² + 1×2¹ + 1×2⁰ + 1×2⁻¹ + 0×2⁻² + 1×2⁻³ = 16 + 8 + 0 + 2 + 1 + 0.5 + 0 + 0.125 = (27.625)₁₀ -
八进制转十进制
(136.524)₈ = 1×8² + 3×8¹ + 6×8⁰ + 5×8⁻¹ + 2×8⁻² + 4×8⁻³ = 64 + 24 + 6 + 0.625 + 0.03125 + 0.0078125 = (94.6640625)₁₀ -
十六进制转十进制
(AB)₁₆ = 10×16¹ + 11×16⁰ = 160 + 11 = (171)₁₀
2.十进制 -> n进制
十进制转换成其他进制时,需分两部分进行,即整数部分和小数部分
- 十进制(25)10(25)10转二进制
1 | 25 / 2 = 12 ....1 |
- 十进制(25)10(25)10转八进制
1 | 25 / 8 = 3 ....1 |
- 十进制(255)10(255)10转十六进制
1 | 255 / 16 = 15 ....15(F) |
3. 编码基础与数据单位
编码是将信息(如数字、字母、符号)转换为特定二进制格式的过程。这种用于在数字系统中表示信息的二进制表示形式,称为代码(Code)。
基本数据单位
计算机处理和存储信息时,使用以下基本单位:
- 比特 (Bit):binary digit 的缩写,是计算机中表示信息的最小单位,其值为
0或1 - 字节 (Byte):最常用的基本单位,固定为8个比特 (8 bit)。它是计算机中数据处理和存储的基本单元
- 字 (Word):CPU一次性处理、存取和传送的数据块。一个字所包含的比特数称为字长。字长是衡量计算机性能的重要指标,通常是字节的整数倍,如16位(2字节)、32位(4字节)、64位(8字节)
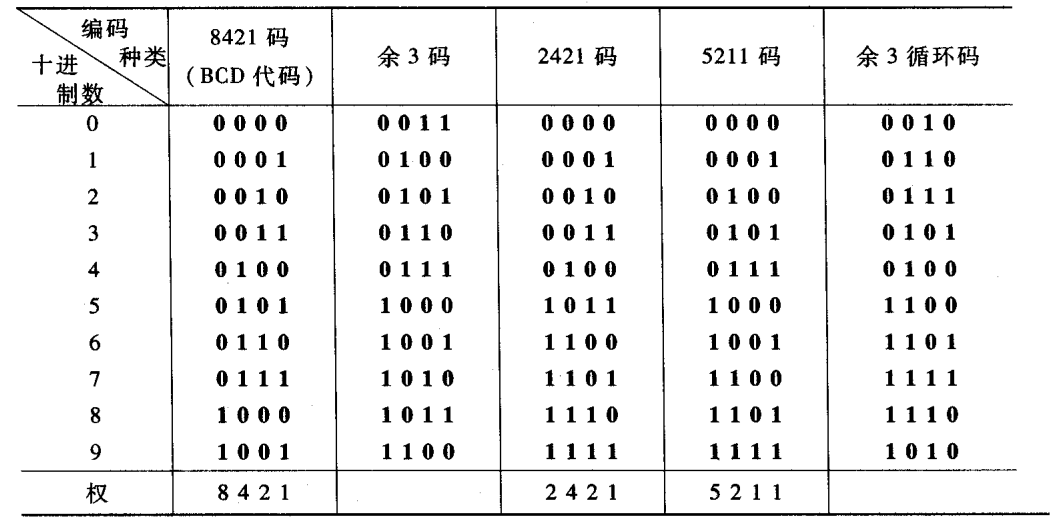
4. 常见编码方案
1. BCD码
BCD码(Binary-Coded Decimal)是一种用4位二进制数来独立表示每一位十进制数(0-9)的编码方式。它主要用于需要精确表示十进制数的场合,如计算器或电子显示。
- 8421 BCD码: 这是最常用的一种BCD码,它是一种有权码。4个比特位的权值从高到低分别为8、4、2、1。例如,十进制数
9表示为1001
2. ASCII码
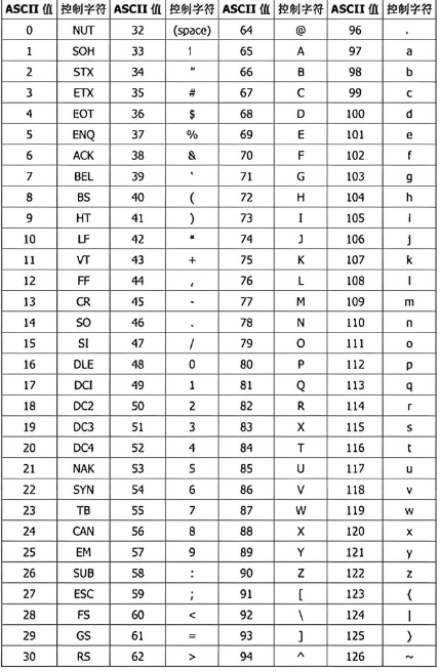
ASCII (American Standard Code for Information Interchange) 是目前最通用的字符编码标准,用于在计算机中表示文本信息。
- 核心特点: 它使用7位二进制数来表示 128个 不同的字符,包括大/小写英文字母、数字0-9、标点符号以及一些特殊的控制字符。
逻辑代数
逻辑代数是分析和设计数字逻辑电路的数学工具。它使用变量来表示逻辑状态(1代表“真”,0代表“假”),并通过与(AND)、或(OR)、**非(NOT)**三种基本运算来描述事物间的因果关系。逻辑代数中的0和1不表示数值大小,仅代表两种对立的逻辑状态
1.逻辑代数运算
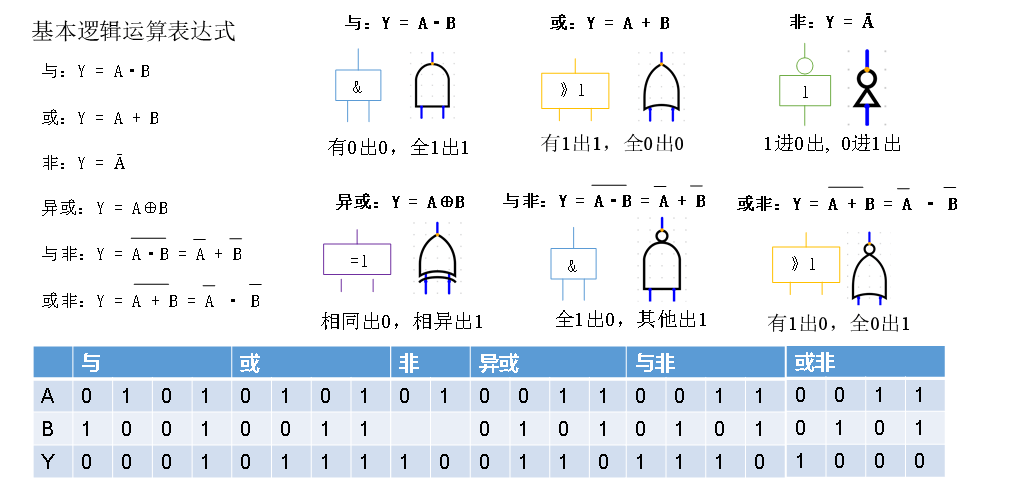
逻辑代数的基本运算有与(AND)、或(OR)、非(NOT)三种
下图为与或非三种逻辑对应电路图示
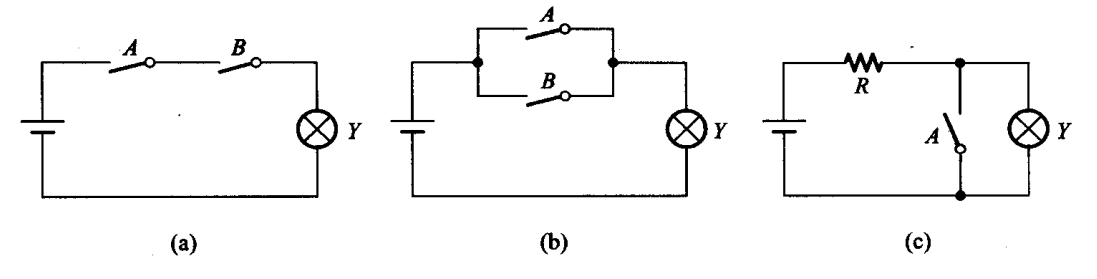
每种逻辑运算都可以通过逻辑表达式、真值表和逻辑符号来描述。
1. 与 (AND)
- 逻辑功能: 当所有输入条件都为
1时,输出才为1。可以理解为“串联”关系。 - 逻辑表达式:
Y = A · B(或Y = AB) - 真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. 或 (OR)
- 逻辑功能: 只要有任意一个输入条件为
1,输出就为1。可以理解为“并联”关系。 - 逻辑表达式:
Y = A + B - 真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. 非 (NOT)
- 逻辑功能: 输出与输入的状态完全相反。也称为“反相”。
- 逻辑表达式: Y = A’ (或 )
- 真值表:
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
逻辑符号
 2. 公式
2. 公式
逻辑代数遵循一系列定律和公式,可用于简化复杂的逻辑表达式。
1. 基本公式
- 与0和1的运算:
A + 0 = AA · 1 = AA + 1 = 1A · 0 = 0
- 与自身的运算:
A + A = AA · A = A
- 与反变量的运算:
A +A’= 1A ·A’= 0
- 双重否定:
- (A’)’
= A
- (A’)’
2. 基本定律
- 交换律:
A + B = B + A|A · B = B · A - 结合律:
(A + B) + C = A + (B + C)|(A · B) · C = A · (B · C) - 分配律:
A · (B + C) = A · B + A · C
3. 重要规则
- 吸收律:
A + A · B = A|A · (A + B) = A - 德·摩根定律 (De Morgan’s Laws):
3. 逻辑函数
逻辑函数是描述输入逻辑变量与输出结果之间因果关系的数学表达式,一般写作 Y = f(A, B, C, ...)。任何复杂的逻辑关系都可以通过逻辑函数来描述。
逻辑函数表示方法
一个逻辑函数有三种标准表示方法:
- 逻辑函数式: 使用与、或、非等运算符构成的代数表达式。
- 逻辑真值表: 枚举所有输入变量的取值组合,并列出每种组合对应的输出值。
- 逻辑图: 使用标准的逻辑门符号,将逻辑表达式的运算关系用图形化方式连接起来。
示例:举重裁判电路
-
逻辑需求: 共有三名裁判:主裁判A,副裁判B和C。当主裁判A同意,并且至少一名副裁判(B或C)同意时,试举成功(输出Y为1)。
-
1. 逻辑函数式:
根据需求,“B或C同意”表示为(B + C)。“A同意”与上述条件同时满足,表示为“与”运算。因此,函数式为:
Y = A · (B + C) -
2. 逻辑真值表:
| A | B | C | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
- 3. 逻辑图:
门电路
用以实现基本逻辑运算和复合逻辑运算的单元电路称为门电路
将实现与逻辑运算的单元电路称为与门电路,将实现或逻辑运算的单元电路称为或门电路,将实现非逻辑运算的单元电路称为非门电路(也称为反相器)。
软件推荐
为了学习这些门电路,我们可以使用数字电路仿真软件,对这些门电路进行仿真加深理解。
官方网站:https://github.com/hneemann/Digital
安装完成后打开digital,看到如下页面即安装成功:
门电路是实现基本逻辑运算的物理电子单元。根据其技术实现和逻辑功能,可以从不同维度进行分类
1. 按实现技术分类 (TTL vs. CMOS)
数字电路从早期的分立元件(如单个二极管、三极管)发展到今天的集成电路 (IC),其中所有元件都制作在一块半导体芯片上。在集成电路技术中,主要有两种主流的逻辑门系列:
| 特性 | TTL (晶体管-晶体管逻辑) | CMOS (互补金属氧化物半导体) |
|---|---|---|
| 核心优势 | 速度快 | 功耗极低 |
| 功耗 | 较高,即使在静态时也有功耗 | 极低,几乎只在开关状态切换时才消耗功率 |
| 集成度 | 较低,因功耗和发热问题受限 | 极高,低功耗特性使其可以实现超大规模集成(VLSI) |
| 当前地位 | 逐渐淘汰 | 当今数字集成电路的绝对主流技术 |
结论: 尽管早期的TTL电路在速度上有优势,但其高功耗的致命缺点限制了集成规模。CMOS技术凭借其极低功耗的巨大优势,实现了极高的集成度,并且随着工艺进步,其速度也得到了极大提升,最终成为现代数字电子技术的基础。
2. 按逻辑功能分类
基础逻辑电路
- 定义: 实现单一、基本逻辑运算的最小电路单元,是构成所有复杂数字系统的基础。
- 特点: 功能原子性,不可再分解。
- 示例: 与门、或门、非门、与非门、或非门、异或门等。
组合逻辑电路
- 定义: 由多个基础逻辑门组合而成,用以实现特定、更复杂逻辑功能的电路。
- 核心特点: 电路的输出仅取决于当前的输入信号状态,与电路过去的状态无关。它没有记忆功能。
- 示例: 加法器、减法器、编码器、解码器、数据选择器等。
基础逻辑门电路总结
运算器
运算器是由逻辑门构成的、用于执行算术和逻辑运算的组合逻辑电路。
1. 半加器
功能:
半加器是实现两个1位二进制数相加的最基本电路。它不考虑来自低位的进位。
输入与输出:
- 输入: 两个加数 A 和 B。
- 输出:
- 本位和 (S): A 与 B 相加的结果。
- 向高位的进位 (Cout): A 与 B 相加产生的进位。
真值表:
通过分析1位二进制加法的所有可能,可以得到如下真值表:
| 输入 A | 输入 B | 进位 Cout | 本位和 S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
逻辑表达式与电路实现:
根据真值表可以推导出:
- 本位和 (S) 的逻辑关系是 异或
- 进位 (Cout) 的逻辑关系是 与
因此,逻辑表达式为:
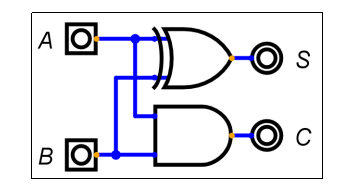
S = A ⊕ BCout = A · B
这表明半加器可以由一个 异或门 和一个 与门 构成。
逻辑图:
2. 全加器
功能:
半加器无法处理来自低位的进位,因此不能直接用于多位加法。全加器是功能更完整的1位加法单元,它能对三个1位二进制数进行相加。
输入与输出:
- 输入:
- 两个加数 A 和 B。
- 来自低位的进位 Cin (Carry-in)。
- 输出:
- 本位和 (S)。
- 向高位的进位 Cout (Carry-out)。
真值表与逻辑表达式:
| A | B | Cin | Cout | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
由真值表可得逻辑表达式:
S = A ⊕ B ⊕ CinCout = (A · B) + (Cin · (A ⊕ B))
电路实现:
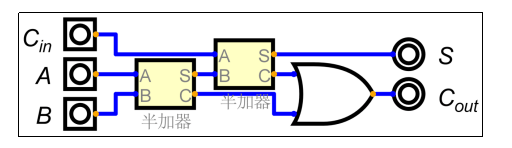
一个全加器可以由两个半加器和一个或门构成。
- 第一个半加器计算
A + B,得到中间和S1和进位C1。 - 第二个半加器计算
S1 + Cin,得到最终和S和进位C2。 - 最终的进位
Cout是两个中间进位C1和C2的或。
逻辑图:
3. 多位加法器
功能:
通过将多个1位全加器串联起来,即可构成一个多位加法器。这种结构被称为行波进位加法器 (Ripple-Carry Adder)。
工作原理:
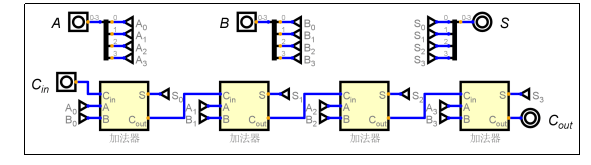
对于一个N位的加法器,需要N个全加器。第 i 位的全加器的进位输出 Cout,连接到 第 i+1 位的全加器的进位输入 Cin。这样,进位信号就像波浪一样从最低位传递到最高位。
4位行波进位加法器逻辑图:
4. 减法器
核心原理:通过补码将减法转换为加法
在数字电路中,减法运算 A - B 通常通过计算 A + (-B) 来实现。-B 在二进制中通过其补码 来表示。
求补码的规则:
将一个二进制数所有位取反,然后在末位加1。
加/减法器电路:
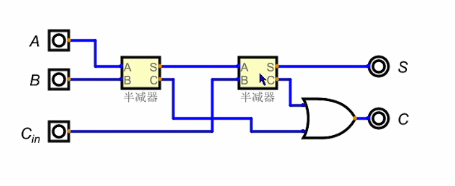
利用这个原理,我们可以在多位加法器的基础上稍作修改,构建一个既能执行加法也能执行减法的电路。
- 引入一个控制信号
Sub。当Sub=0时执行加法,当Sub=1时执行减法。 - 使用 XOR (异或门) 作为可控反相器。当
Sub=0时,B ⊕ 0 = B(B不变);当Sub=1时,B ⊕ 1 = B'(B取反)。 - 将
Sub信号同时连接到最低位的进位输入Cin。
工作流程:
- 加法 (Sub=0): XOR门输出B,
Cin为0。电路执行A + B + 0。 - 减法 (Sub=1): XOR门输出B的反码
B',Cin为1。电路执行A + B' + 1,这正好是A加上B的补码,从而实现了减法。
逻辑图:
时序逻辑电路:
锁存器、触发器与寄存器
与输出仅取决于当前输入的组合逻辑电路不同,时序逻辑电路的输出不仅取决于当前输入,还与电路之前的状态有关。这是因为它们包含了存储元件,能够“记忆”信息。锁存器和触发器是构成所有时序电路最基本的存储单元。
核心概念:锁存器 vs. 触发器
- 锁存器 (Latch): 电平敏感 (Level-Sensitive) 器件。当控制信号(使能端En)处于有效电平(通常是高电平)时,输出会跟随输入变化,就像一个打开的“门”,此时称之为“透明”状态。当控制信号无效时,“门”关闭,输出保持最后的状态。
- 触发器 (Flip-Flop): 边沿敏感 (Edge-Sensitive) 器件。它的状态仅在时钟信号(CLK)的特定边沿(上升沿
↑或下降沿↓)发生跳变时才可能改变。在时钟信号的其他所有时刻,输出都保持不变,这使其比锁存器更稳定、更适合构建同步数字系统。
1. 基本SR锁存器 (SR Latch)
最基础的存储单元,由两个交叉耦合的或非门(或与非门)构成。
- 功能: 具有“置位”(Set)和“复位”(Reset)功能。
- 输入:
S(Set): 置位端。当S=1时,强制输出Q为1。R(Reset): 复位端。当R=1时,强制输出Q为0。
- 逻辑图 (或非门):
* 功能表:
| S | R | Q (Next State) | 说明 |
|---|---|---|---|
| 0 | 0 | Q (Current) | 保持 (Hold) |
| 0 | 1 | 0 | 复位 (Reset) |
| 1 | 0 | 1 | 置位 (Set) |
| 1 | 1 | ? | 无效/禁用状态 |
- 问题: 存在
S=R=1的禁用状态,且状态的改变是即时的,不易控制。
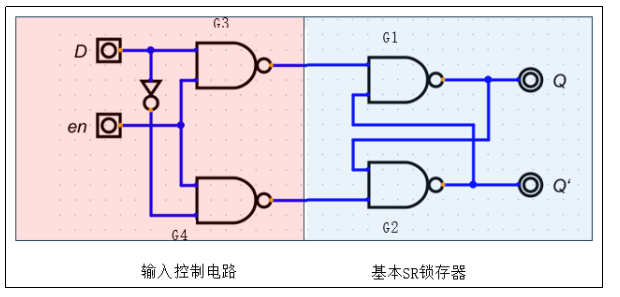
2. D锁存器 (D Latch)
在SR锁存器的基础上增加了一个使能端 (Enable, E) 并解决了禁用状态问题,是实际应用中最常见的锁存器。
- 功能: 在使能信号有效时,将数据输入
D的值传递到输出Q;在使能信号无效时,锁存Q的值。 - 逻辑图:
- 功能表:
| E | D | Q (Next State) | 说明 |
|---|---|---|---|
| 0 | X | Q (Current) | 锁存/保持 |
| 1 | 0 | 0 | 透明,输出为0 |
| 1 | 1 | 1 | 透明,输出为1 |
- 问题: 在
E=1期间,输出Q会完全跟随输入D的任何波动,这种“透明性”在复杂的同步电路中可能引发问题。
3. D触发器 (D Flip-Flop)
D触发器是数字系统中使用最广泛的存储单元,它解决了D锁存器的“透明”问题。
- 功能: 仅在时钟(CLK)的有效边沿(通常是上升沿),将输入
D的值采样并更新到输出Q。在时钟的其他所有时刻,Q保持不变。 - 逻辑符号: 时钟输入端有一个
>符号,表示它是边沿触发的。
- 功能表 (上升沿触发):
| CLK | D | Q (Next State) | 说明 |
|---|---|---|---|
| ↑ | 0 | 0 | 在时钟上升沿,采样D=0 |
| ↑ | 1 | 1 | 在时钟上升沿,采样D=1 |
| 非↑ | X | Q (Current) | 保持 |
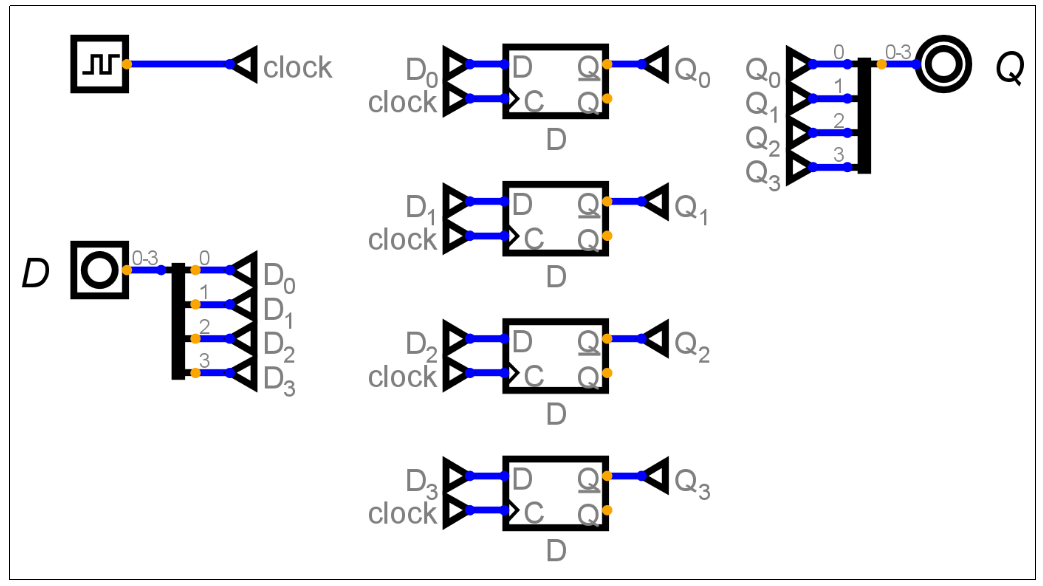
4. 寄存器 (Register)
- 功能: 用于存储一组二进制数据(一个字)。
- 结构: 一个N位寄存器由 N个D触发器 并联构成,它们共享同一个时钟信号,从而可以在同一个时钟边沿同步地锁存N位数据。
- 逻辑图 (4位寄存器):
 2. 公式
2. 公式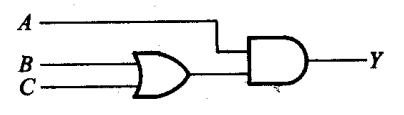

 * 功能表:
* 功能表: